
بحث عن تحليل الدوال … فبداية تحليل الدوال هو جزء من التحليل الرياضي الحديث الذي يتمثل الغرض الأساسي في دراسة الوظائف 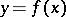 التي هي واحدة على الأقل من المتغيرات
التي هي واحدة على الأقل من المتغيرات  أو
أو 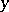 يختلف على مساحة غير محدودة الأبعاد. في شكلها الأكثر عمومية ، تقع هذه الدراسة في ثلاثة أجزاء: 1) إدخال ودراسة المساحات اللانهائية الأبعاد على هذا النحو ؛ 2) دراسة أبسط الوظائف ، أي متى
يختلف على مساحة غير محدودة الأبعاد. في شكلها الأكثر عمومية ، تقع هذه الدراسة في ثلاثة أجزاء: 1) إدخال ودراسة المساحات اللانهائية الأبعاد على هذا النحو ؛ 2) دراسة أبسط الوظائف ، أي متى  يأخذ القيم في الفضاء اللامتناهي الابعاد و
يأخذ القيم في الفضاء اللامتناهي الابعاد و 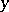 في الفضاء أحادي البعد (تسمى هذه الوظائف (cf. Functional ) ، من حيث الاسم “تحليل الدوال “) ؛ و 3) دراسة الوظائف العامة من النوع المحدد – المشغلين (cf. المشغل ). وظائف خطية
في الفضاء أحادي البعد (تسمى هذه الوظائف (cf. Functional ) ، من حيث الاسم “تحليل الدوال “) ؛ و 3) دراسة الوظائف العامة من النوع المحدد – المشغلين (cf. المشغل ). وظائف خطية 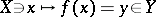 ، أي المشغلين الخطي ، تم دراستها بشكل كامل. نظريتها هي في الأساس تعميم الجبر الخطي لحالة لا نهائية الأبعاد. إن الجمع بين مقاربات التحليل والجبر الكلاسيكي هو سمة مميزة لأساليب تحليل الدوال ، وهذا يؤدي إلى العلاقات بين ما يبدو للوهلة الأولى فروعًا بعيدة جدًا للرياضيات في بحث عن تحليل الدوال.
، أي المشغلين الخطي ، تم دراستها بشكل كامل. نظريتها هي في الأساس تعميم الجبر الخطي لحالة لا نهائية الأبعاد. إن الجمع بين مقاربات التحليل والجبر الكلاسيكي هو سمة مميزة لأساليب تحليل الدوال ، وهذا يؤدي إلى العلاقات بين ما يبدو للوهلة الأولى فروعًا بعيدة جدًا للرياضيات في بحث عن تحليل الدوال.
بدأ تحليل الدوال كنظام رياضي مستقل في مطلع القرن التاسع عشر وأُنشئ أخيرًا في عشرينيات وثلاثينيات القرن العشرين ، من ناحية تحت تأثير دراسة فئات محددة من المشغلين الخطيين – المشغلين المتكاملين والمعادلات المتكاملة المرتبطة بهم – ومن ناحية أخرى تحت تأثير التطور الداخلي المحض للرياضيات الحديثة برغبتها في التعميم ، وبالتالي توضيح الطبيعة الحقيقية لبعض السلوك المنتظم. كان لميكانيكا الكم أيضا تأثير كبير على تطوير تحليل الدوال ، لأن مفاهيمها الأساسية ، على سبيل المثال الطاقة ، تحولت إلى عوامل خطية (التي كان الفيزيائيون في البداية يفسرونها بشكل فضفاض على أنها مصفوفات غير متناهية الأبعاد) على فضاءات غير محدودة الأبعاد.
1. مفهوم الفضاء.
تعتبر مساحات ناقلات الطوبولوجيا (cf.). فضاءات ناقلات الطوبولوجيا هي أكثر المساحات العامة التي يتم تحليلها في تحليل الدوال . هذه مسافات متجهة (خطية) 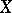 على ميدان الأعداد المركبة
على ميدان الأعداد المركبة 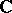 (أو أي حقل آخر ، على سبيل المثال الرقم الحقيقي ،
(أو أي حقل آخر ، على سبيل المثال الرقم الحقيقي ، 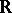 ) وهي مساحات طوبولوجية متزامنة وحيث تكون البنية الخطية والطوبولوجيا متوافقتين بمعنى أن العمليات الخطية مستمرة في الهيكلية قيد النظر. على وجه الخصوص ، إذا
) وهي مساحات طوبولوجية متزامنة وحيث تكون البنية الخطية والطوبولوجيا متوافقتين بمعنى أن العمليات الخطية مستمرة في الهيكلية قيد النظر. على وجه الخصوص ، إذا 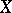 هي مساحة متريّة ، ثمّ لدى المرء مساحة متجه متجهية.
هي مساحة متريّة ، ثمّ لدى المرء مساحة متجه متجهية.
وينشأ وضع أكثر خصوصية ، ولكنه هام للغاية ، عندما يكون مفهوم القاعدة 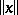 (طول) المتجه
(طول) المتجه 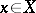 يتم تقديمه بشكل محوري في الفضاء المتجه
يتم تقديمه بشكل محوري في الفضاء المتجه 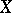 . تُسمى المساحة المتجهة مع القاعدة مساحة قياسية. فمن metrizable. مقياس
. تُسمى المساحة المتجهة مع القاعدة مساحة قياسية. فمن metrizable. مقياس 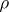 هو المقدمة من الصيغة:
هو المقدمة من الصيغة: 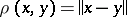 . تُسمى مساحة المتجه مع القاعدة مساحة Banach إذا كانت مكتملة فيما يتعلق بالمقياس المشار إليه.
. تُسمى مساحة المتجه مع القاعدة مساحة Banach إذا كانت مكتملة فيما يتعلق بالمقياس المشار إليه.
في عدد كبير من المشاكل تنشأ الحالة حيث يمكن للمرء إدخال منتج داخلي 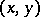 لأي متجهين في الفضاء الموجه
لأي متجهين في الفضاء الموجه 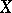 ، بحيث هذا المنتج يعمم المنتج القياسي المعتاد في الفضاء ثلاثي الأبعاد. تسمى المساحة المزودة بمنتج داخلي بمساحة ما قبل هيلبرت. إنها حالة خاصة من الفضاء المعياري. إذا كانت هذه المساحة مكتملة ، فسيتم تسميتها بمساحة هيلبرت.
، بحيث هذا المنتج يعمم المنتج القياسي المعتاد في الفضاء ثلاثي الأبعاد. تسمى المساحة المزودة بمنتج داخلي بمساحة ما قبل هيلبرت. إنها حالة خاصة من الفضاء المعياري. إذا كانت هذه المساحة مكتملة ، فسيتم تسميتها بمساحة هيلبرت.
تتم دراسة المساحات اللانهائية الأبعاد في تحليل الدوال ، أي الفراغات التي توجد بها مجموعة لا نهائية من النواقل المستقلة خطيًا.
من وجهة النظر الهندسية فإن أبسط المساحات هي مساحات هيلبرت  التي لها خصائص تشبه في الغالب المسافات ذات الأبعاد المحدودة ، لأنه من الممكن إدخال مفهوم مشابه لمفهوم الزاوية بين متجهين عن طريق المنتج الداخلي. على وجه الخصوص ، اثنين من المتجهات
التي لها خصائص تشبه في الغالب المسافات ذات الأبعاد المحدودة ، لأنه من الممكن إدخال مفهوم مشابه لمفهوم الزاوية بين متجهين عن طريق المنتج الداخلي. على وجه الخصوص ، اثنين من المتجهات 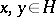 يقال أن تكون متعامدة
يقال أن تكون متعامدة 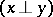 إذا
إذا 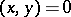 . النتيجة التالية صحيحة في
. النتيجة التالية صحيحة في  : دعونا
: دعونا  يكون فضاء جزئي من
يكون فضاء جزئي من 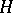 ، ثم أي ناقل
، ثم أي ناقل 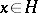 لديه إسقاط
لديه إسقاط 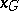 على
على 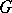 ، وهذا هو ، ناقل
، وهذا هو ، ناقل 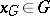 مثل ذلك
مثل ذلك 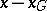 هو متعامد لأي متجه في
هو متعامد لأي متجه في 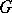 . وبسبب هذه الحقيقة ، يمكن نقل عدد كبير من المنشآت الهندسية التي تحمل مساحات محدودة الأبعاد إلى فضاء هيلبرت ، حيث تكتسب في كثير من الأحيان شخصية تحليلية.
. وبسبب هذه الحقيقة ، يمكن نقل عدد كبير من المنشآت الهندسية التي تحمل مساحات محدودة الأبعاد إلى فضاء هيلبرت ، حيث تكتسب في كثير من الأحيان شخصية تحليلية.
تصبح الأسئلة الهندسية أكثر تعقيدًا بشكل واضح عند الانتقال من فضاء هيلبرت إلى مساحات باناخ ، وأكثر من ذلك في فضاءات ناقلات الطوبولوجيا العامة ، لأن الإسقاط المتعامد ليس له مغزى فيها. على سبيل المثال ، في الفضاء 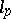 (
( 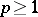 ) المتجهات
) المتجهات 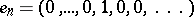 تشكل أساسا بمعنى أنه لكل متجه
تشكل أساسا بمعنى أنه لكل متجه 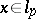 توسيع “التنسيق – الحكيم” صالح:
توسيع “التنسيق – الحكيم” صالح:
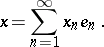 |
بناء أساس للمساحة 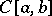 هو بالفعل أكثر تعقيدا قليلا. في نفس الوقت يمكن بناء الأساس في كل من الأمثلة المعروفة لمساحات Banach. نشأت المشكلة: هل هناك أساس في كل مساحة Banach؟ هذه المشكلة ، على الرغم من الجهود التي بذلها العديد من علماء الرياضيات ، لم تسفر عن حل لأكثر من 40 عامًا ، ولم تحل سلبًا إلا في عام 1972 (راجع [23] ). في تحليل الدوال ، يتم احتلال مكان مهم بمواضيع “هندسية” ، مكرسة لتوضيح خصائص مجموعات مختلفة في Banach ومساحات أخرى ، على سبيل المثال مجموعات محدبة ، مجموعات مدمجة (هذا الأخير يعني أن كل تسلسل لنقاط مثل هذه المجموعة
هو بالفعل أكثر تعقيدا قليلا. في نفس الوقت يمكن بناء الأساس في كل من الأمثلة المعروفة لمساحات Banach. نشأت المشكلة: هل هناك أساس في كل مساحة Banach؟ هذه المشكلة ، على الرغم من الجهود التي بذلها العديد من علماء الرياضيات ، لم تسفر عن حل لأكثر من 40 عامًا ، ولم تحل سلبًا إلا في عام 1972 (راجع [23] ). في تحليل الدوال ، يتم احتلال مكان مهم بمواضيع “هندسية” ، مكرسة لتوضيح خصائص مجموعات مختلفة في Banach ومساحات أخرى ، على سبيل المثال مجموعات محدبة ، مجموعات مدمجة (هذا الأخير يعني أن كل تسلسل لنقاط مثل هذه المجموعة 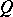 لديها بعد تقارب إلى نقطة في
لديها بعد تقارب إلى نقطة في 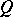 ) ، إلخ. هنا ، الأسئلة ذات الصياغة البسيطة غالباً ما تكون لها حلول غير تافهة. ترتبط هذه المشكلات ارتباطًا وثيقًا بدراسة التماثل بين المساحات ، وإيجاد ممثلين عالميين في بعض فئات المساحات.
) ، إلخ. هنا ، الأسئلة ذات الصياغة البسيطة غالباً ما تكون لها حلول غير تافهة. ترتبط هذه المشكلات ارتباطًا وثيقًا بدراسة التماثل بين المساحات ، وإيجاد ممثلين عالميين في بعض فئات المساحات.
تمت دراسة مساحات وظيفية محددة بالتفصيل ، لأن خصائص هذه المساحات تحدد عادة طبيعة الحل لمشكلة عندما يتم الحصول عليها بواسطة طرق تحليل الدوال. ما يسمى نظريات impleding لمساحات Sobolev 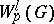 ،
، 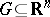 ، ومختلف التعميمات من هذه ، يمكن أن تكون مثالا على ذلك.
، ومختلف التعميمات من هذه ، يمكن أن تكون مثالا على ذلك.
فيما يتعلق بمتطلبات الفيزياء الرياضية الحديثة ، نشأ عدد كبير من المساحات المحددة التي تطرح فيها المشاكل بشكل طبيعي وبالتالي يجب دراستها. عادة ما يتم إنشاء هذه المساحات من المساحات الأولية باستخدام منشآت معينة. تحت الإنشاءات الأكثر استخداما يتم تقديمها في أبسط صيغها.
1) تشكيل مبلغ متعامد 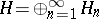 من الفضاء هيلبرت
من الفضاء هيلبرت 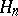 ،
، 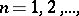 هو بناء الفضاء
هو بناء الفضاء 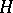 من حيث المساحات
من حيث المساحات 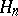 ، على غرار تشكيل
، على غرار تشكيل 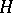 من حيث المسافات أحادية البعد.
من حيث المسافات أحادية البعد.
2) الانتقال إلى حيز الحصة: نظرا للمنتج الداخلي المتدهور  في الفضاء المتجه
في الفضاء المتجه 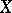 (هذا هو،
(هذا هو، 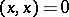 ممكن عندما
ممكن عندما 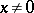 )؛ الفضاء هيلبرت
)؛ الفضاء هيلبرت 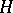 يعرف بأنه الانتهاء من
يعرف بأنه الانتهاء من 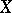 بالنسبة إلى
بالنسبة إلى 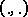 بعد التعرف أولا على 0 جميع تلك المتجهات
بعد التعرف أولا على 0 جميع تلك المتجهات 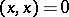 .
.
3) تشكيل منتج موتر 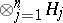 هو مماثل لتمرير من وظائف متغير واحد
هو مماثل لتمرير من وظائف متغير واحد 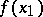 إلى وظائف عدة متغيرات
إلى وظائف عدة متغيرات 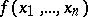 . يستخدم بناء مشابه أيضًا لعدد لا حصر له من العوامل ؛ ينظر المرء أيضاً إلى المنتجات المتناظرة المتماثلة والمضادة للاتساق التي تتكون ، في حالة الوظائف ، من وظائف عدة متغيرات لها هذه الخصائص.
. يستخدم بناء مشابه أيضًا لعدد لا حصر له من العوامل ؛ ينظر المرء أيضاً إلى المنتجات المتناظرة المتماثلة والمضادة للاتساق التي تتكون ، في حالة الوظائف ، من وظائف عدة متغيرات لها هذه الخصائص.
4) تشكيل الحد الإسقاطي 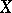 من مساحات Banach
من مساحات Banach 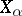 ، أين
، أين 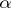 يعمل على مجموعة معينة من المؤشرات
يعمل على مجموعة معينة من المؤشرات 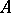 . حسب التعريف،
. حسب التعريف، 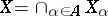 . الطوبولوجيا في
. الطوبولوجيا في 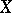 ، تقريبا ، من خلال التقارب
، تقريبا ، من خلال التقارب 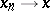 مما يعنى
مما يعنى  فيما يتعلق بالقاعدة في كل
فيما يتعلق بالقاعدة في كل 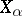 .
.
5) تشكيل الحد الاستقرائي 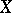 من مساحات Banach
من مساحات Banach 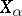 . حسب التعريف،
. حسب التعريف، 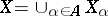 . الطوبولوجيا في
. الطوبولوجيا في 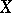 ، تقريبا ، من خلال التقارب
، تقريبا ، من خلال التقارب  مما يعني أن كل
مما يعني أن كل 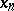 تكمن في معين
تكمن في معين 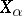 وذلك
وذلك 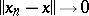 فيما يتعلق بقاعدة هذا الفضاء.
فيما يتعلق بقاعدة هذا الفضاء.
6) الاستيفاء هو تشكيل المساحات “المتوسطة” 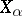 من مكانين
من مكانين 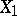 و
و 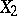 ، أين
، أين 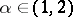 . على سبيل المثال ، البناء من
. على سبيل المثال ، البناء من 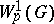 و
و 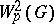 من الفضاء
من الفضاء 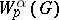 من الوظائف مع مشتق كسور
من الوظائف مع مشتق كسور 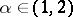 .
.
يتم تطبيق الإجراءات 4) و 5) عادة عند بناء مساحات ناقلات طوبولوجية. يميز المرء بين هذه الفراغات الفئة المهمة جداً من المساحات النووية المسماة (راجع الفضاء النووي ) ، كل منها مبني كحد إسقاطى لمساحات هيلبرت 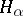 مع الخاصية التي ، لكل
مع الخاصية التي ، لكل 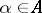 يمكن للمرء أن يجد
يمكن للمرء أن يجد 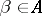 مثل ذلك
مثل ذلك 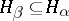 والمشغل إمبلاديدينج
والمشغل إمبلاديدينج 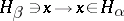 هو مشغل هيلبرت شميدت (انظر أدناه ، القسم
هو مشغل هيلبرت شميدت (انظر أدناه ، القسم  ).
).
وقد تم تطوير فرع كبير ومهم من تحليل الدوال والذي يقوم فيه المرء بدراسة مساحات ناقلات طوبولوجية ومعايير مع ترتيب جزئي ، يتم إدخاله بشكل بصري ، وله خصائص طبيعية (مسافات مرتبة جزئيا).
2. وظائف في بحث عن تحليل الدوال
في تحليل الدوال ، تلعب دراسة الوظائف المستمرة والوظائف الخطية دوراً أساسياً (راجع وظيفية مستمرة ؛ وظيفية خطية ) ؛ ترتبط ارتباطا وثيقا خصائصها مع خصائص الفضاء الأصلي 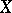 .
.
سمح 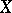 تكون مساحة Banach والسماح
تكون مساحة Banach والسماح 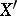 تكون مجموعة من الدالات الخطية المستمرة عليها ؛
تكون مجموعة من الدالات الخطية المستمرة عليها ؛ 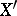 هي مساحة متجهة فيما يتعلق بالعمليات المعتادة لإضافة وظائف وضربها بواسطة رقم ، تصبح مساحة Banach إذا قدمنا القاعدة
هي مساحة متجهة فيما يتعلق بالعمليات المعتادة لإضافة وظائف وضربها بواسطة رقم ، تصبح مساحة Banach إذا قدمنا القاعدة
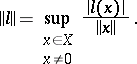 |
الفضاء  يسمى الثنائي
يسمى الثنائي 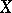 (راجع أيضًا الفضاء المجاور ).
(راجع أيضًا الفضاء المجاور ).
إذا  هو متناهية الأبعاد ، ثم كل وظيفية خطية هي من الشكل
هو متناهية الأبعاد ، ثم كل وظيفية خطية هي من الشكل
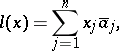 |
أين 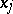 هي إحداثيات المتجه
هي إحداثيات المتجه  فيما يتعلق على أساس معين و
فيما يتعلق على أساس معين و 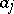 هي الأرقام التي تحددها الوظيفية. اتضح أن الصيغة تحمل أيضا متى
هي الأرقام التي تحددها الوظيفية. اتضح أن الصيغة تحمل أيضا متى 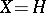 هي مساحة هيلبرت (نظرية رييز). وهي في هذه الحالة
هي مساحة هيلبرت (نظرية رييز). وهي في هذه الحالة 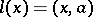 ، أين
، أين  هو متجه معين في
هو متجه معين في 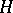 . توضح هذه الصيغة أن مساحة هيلبرت تتزامن في الأساس مع ثنائيها.
. توضح هذه الصيغة أن مساحة هيلبرت تتزامن في الأساس مع ثنائيها.
بالنسبة إلى مساحة باناخ ، فإن الوضع أكثر تعقيدًا: يمكن للمرء أن يبني 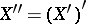 ،
، 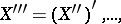 وهذه المساحات قد تكون مختلفة. في نفس الوقت ، هناك دائما وجود impleding الكنسي
وهذه المساحات قد تكون مختلفة. في نفس الوقت ، هناك دائما وجود impleding الكنسي 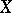 إلى
إلى 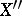 ، أي لكل منهما
، أي لكل منهما 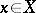 يمكن للمرء أن ربط الوظيفية
يمكن للمرء أن ربط الوظيفية 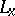 ، أين
، أين 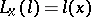 ،
، 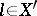 . المساحات
. المساحات 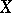 لأي منهم
لأي منهم 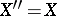 تسمى الانعكاسية. بشكل عام ، في حالة وجود مساحة Banach ، فإن وجود وظائف خطية غير تافهة (أي غير صفرية) ليس سؤالًا بسيطًا. تم حل هذا السؤال بسهولة بالإيجاب بمساعدة نظرية هان-باناخ .
تسمى الانعكاسية. بشكل عام ، في حالة وجود مساحة Banach ، فإن وجود وظائف خطية غير تافهة (أي غير صفرية) ليس سؤالًا بسيطًا. تم حل هذا السؤال بسهولة بالإيجاب بمساعدة نظرية هان-باناخ .
الفضاء المزدوج 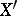 بمعنى ما ، “أفضل” من المساحة الأصلية
بمعنى ما ، “أفضل” من المساحة الأصلية 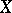 . على سبيل المثال ، إلى جانب المعيار يمكن إدخال طبولوجيا أخرى (ضعيفة) في
. على سبيل المثال ، إلى جانب المعيار يمكن إدخال طبولوجيا أخرى (ضعيفة) في 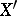 التي ، من حيث التقارب ، هي مثل هذا
التي ، من حيث التقارب ، هي مثل هذا 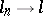 إذا
إذا 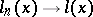 للجميع
للجميع  . في هذه الطبولوجيا وحدة الكرة في
. في هذه الطبولوجيا وحدة الكرة في 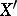 مضغوط (وهو ما لا ينطبق أبداً على المساحات اللامتناهية الأبعاد في الهيكل المولَّدة بقاعدة). هذا يجعل من الممكن دراسة بمزيد من التفصيل عددا من الأسئلة الهندسية حول مجموعات في الفضاء المزدوج (على سبيل المثال ، إنشاء بنية مجموعات محدبة ، الخ).
مضغوط (وهو ما لا ينطبق أبداً على المساحات اللامتناهية الأبعاد في الهيكل المولَّدة بقاعدة). هذا يجعل من الممكن دراسة بمزيد من التفصيل عددا من الأسئلة الهندسية حول مجموعات في الفضاء المزدوج (على سبيل المثال ، إنشاء بنية مجموعات محدبة ، الخ).
لعدد من المساحات المحددة 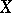 الفضاء المزدوج
الفضاء المزدوج 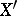 يمكن العثور عليها صراحة. ومع ذلك ، بالنسبة لغالبية مساحات Banach ، وخاصةً في مساحات ناقلات الطوبولوجيا ، فإن الوظائف هي عناصر من نوع جديد لا يمكن التعبير عنه ببساطة من حيث التحليل الكلاسيكي. تسمى عناصر المساحة المزدوجة بالوظائف العامة.
يمكن العثور عليها صراحة. ومع ذلك ، بالنسبة لغالبية مساحات Banach ، وخاصةً في مساحات ناقلات الطوبولوجيا ، فإن الوظائف هي عناصر من نوع جديد لا يمكن التعبير عنه ببساطة من حيث التحليل الكلاسيكي. تسمى عناصر المساحة المزدوجة بالوظائف العامة.
بالنسبة للعديد من الأسئلة في تحليل الدوال
وتطبيقاته ، يتم لعب دور أساسي بواسطة ثلاث مسافات 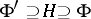 ، أين
، أين 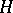 هي مساحة هيلبرت الأصلية ،
هي مساحة هيلبرت الأصلية ، 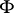 هي مساحة ناقلة طوبولوجية (على وجه الخصوص ، مساحة هيلبرت مع منتج داخلي مختلف) و
هي مساحة ناقلة طوبولوجية (على وجه الخصوص ، مساحة هيلبرت مع منتج داخلي مختلف) و 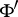 هو الفضاء المزدوج ، ويمكن اعتبار عناصرها كوظائف معممة. الفضاء
هو الفضاء المزدوج ، ويمكن اعتبار عناصرها كوظائف معممة. الفضاء 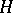 يسمى في حد ذاته مساحة هيلبرت مزورة.
يسمى في حد ذاته مساحة هيلبرت مزورة.
دراسة الوظائف الخطية على 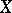 في كثير من النواحي يعزز فهم أعمق لطبيعة الفضاء الأصلي
في كثير من النواحي يعزز فهم أعمق لطبيعة الفضاء الأصلي 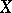 . من ناحية أخرى ، في العديد من الأسئلة ، من الضروري دراسة الوظائف العامة
. من ناحية أخرى ، في العديد من الأسئلة ، من الضروري دراسة الوظائف العامة 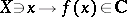 ، وهذا هو ، وظائف غير خطية في حالة لا نهائية الأبعاد
، وهذا هو ، وظائف غير خطية في حالة لا نهائية الأبعاد 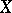 (راجع وظيفية غير خطية ). منذ الكرة وحدة في مثل هذا الفضاء
(راجع وظيفية غير خطية ). منذ الكرة وحدة في مثل هذا الفضاء 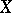 غير مضغوط ، وغالبا ما تواجه دراستها الصعوبات الأساسية ، على الرغم ، على سبيل المثال ، مثل مفاهيم مثل اختلاف
غير مضغوط ، وغالبا ما تواجه دراستها الصعوبات الأساسية ، على الرغم ، على سبيل المثال ، مثل مفاهيم مثل اختلاف 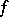 ، التحليلية ، وما إلى ذلك هي معممة بسهولة. يمكن للمرء أن تنظر في مجموعة من الوظائف
، التحليلية ، وما إلى ذلك هي معممة بسهولة. يمكن للمرء أن تنظر في مجموعة من الوظائف 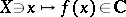 وجود خصائص محددة كمساحة ناقلة طوبولوجية جديدة لوظائف “عدد لا نهائي من المتغيرات”. مثل هذه الوظائف تظهر أيضا في بناء منتجات متمددة لانهائية
وجود خصائص محددة كمساحة ناقلة طوبولوجية جديدة لوظائف “عدد لا نهائي من المتغيرات”. مثل هذه الوظائف تظهر أيضا في بناء منتجات متمددة لانهائية 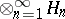 من مسافات وظائف متغير واحد. ترتبط دراسة مثل هذه المساحات ، من المشغلين عليها ، وما إلى ذلك ، بمتطلبات نظرية المجال الكمي (انظر [22] ).
من مسافات وظائف متغير واحد. ترتبط دراسة مثل هذه المساحات ، من المشغلين عليها ، وما إلى ذلك ، بمتطلبات نظرية المجال الكمي (انظر [22] ).
3. المشغلين
الأهداف الرئيسية للدراسة في تحليل الدوال هي المشغلين 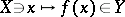 ، أين
، أين 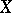 و
و 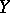 هي ناقلات طوبولوجية (بالنسبة للجزء الأكبر ، أو المعيارية أو هيلبرت) ، وقبل كل شيء ، المشغلين الخطيين (cf. المشغل الخطي ).
هي ناقلات طوبولوجية (بالنسبة للجزء الأكبر ، أو المعيارية أو هيلبرت) ، وقبل كل شيء ، المشغلين الخطيين (cf. المشغل الخطي ).
متى 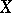 و
و 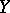 ذات أبعاد محددة ، تشير خطية المشغل إلى أنها من النموذج
ذات أبعاد محددة ، تشير خطية المشغل إلى أنها من النموذج
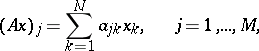 |
أين 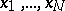 هي إحداثيات المتجه
هي إحداثيات المتجه  على أساس معين ، و
على أساس معين ، و 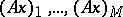 هي ، بشكل مشابه ، إحداثيات
هي ، بشكل مشابه ، إحداثيات 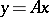 . وهكذا ، في حالة متناهية الأبعاد لكل عامل خطي
. وهكذا ، في حالة متناهية الأبعاد لكل عامل خطي 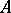 يتوافق ، من حيث القواعد الثابتة في
يتوافق ، من حيث القواعد الثابتة في 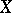 و
و 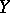 ، مصفوفة
، مصفوفة
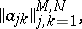 |
الذي يعطي تعبير بسيط ل 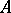 . دراسة العوامل الخطية في هذه الحالة هي موضوع الجبر الخطي.
. دراسة العوامل الخطية في هذه الحالة هي موضوع الجبر الخطي.
يصبح الوضع أكثر تعقيدا عندما 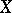 و
و 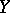 تصبح فراغات لا نهائية الأبعاد (حتى هيلبرت). بادئ ذي بدء ، تنشأ فئتان من المشغلين هنا: المشغلين المتواصلين ، التي تعمل هذه الوظيفة من أجلها
تصبح فراغات لا نهائية الأبعاد (حتى هيلبرت). بادئ ذي بدء ، تنشأ فئتان من المشغلين هنا: المشغلين المتواصلين ، التي تعمل هذه الوظيفة من أجلها 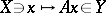 هو مستمر (يُطلق عليه أيضًا اسم “محدد” ، نظرًا لأن استمرارية عامل التشغيل بين مسافات Banach تساوي حده) ، والمشغلين غير المحددين ، حيث لا توجد مثل هذه الاستمرارية. مشغلي النوع الأول هم أبسط ، ولكن يتم تلبية تلك النوع الثاني في كثير من الأحيان ، مثل المشغلين التفاضليين من النوع الثاني.
هو مستمر (يُطلق عليه أيضًا اسم “محدد” ، نظرًا لأن استمرارية عامل التشغيل بين مسافات Banach تساوي حده) ، والمشغلين غير المحددين ، حيث لا توجد مثل هذه الاستمرارية. مشغلي النوع الأول هم أبسط ، ولكن يتم تلبية تلك النوع الثاني في كثير من الأحيان ، مثل المشغلين التفاضليين من النوع الثاني.
المهم (خاصة بالنسبة لميكانيكا الكم) فئة من المشغلين الذاتي في الفضاء هيلبرت 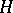 وقد درست أكثر من أي شيء آخر (راجع المشغل ذاتي التوصيل ).
وقد درست أكثر من أي شيء آخر (راجع المشغل ذاتي التوصيل ).
فئات أخرى من المشغلين على 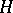 ، تم ربطها بشكل وثيق مع المشغلين ذاتية التوصيل (ما يسمى بالمشغلين الوحدويين والعادية ، cf. المشغل الوراثي ؛ المشغل العادي ) ، تم دراستها أيضًا.
، تم ربطها بشكل وثيق مع المشغلين ذاتية التوصيل (ما يسمى بالمشغلين الوحدويين والعادية ، cf. المشغل الوراثي ؛ المشغل العادي ) ، تم دراستها أيضًا.
من بين الحقائق العامة حول المشغلين المحددين الذين يعملون في مساحة Banach 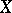 ، يمكن للمرء اختيار بناء حساب التفاضل والتكامل الوظيفي للوظائف التحليلية. أي المشغل
، يمكن للمرء اختيار بناء حساب التفاضل والتكامل الوظيفي للوظائف التحليلية. أي المشغل 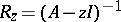 يسمى حل المشغل
يسمى حل المشغل 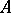 ، أين
، أين 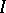 هو مشغل الهوية و
هو مشغل الهوية و 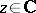 . النقاط
. النقاط  التي المشغل المعاكس
التي المشغل المعاكس 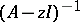 تسمى تسمى النقاط العادية
تسمى تسمى النقاط العادية 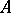 ، وتسمى مجموعة من النقاط العادية الطيف
، وتسمى مجموعة من النقاط العادية الطيف 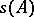 من
من 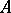 . الطيف ليس خاليا أبدا ويكمن في القرص
. الطيف ليس خاليا أبدا ويكمن في القرص 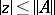 . قيم eigen من
. قيم eigen من 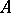 ، بالطبع ، تنتمي إلى
، بالطبع ، تنتمي إلى 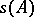 لكن الطيف ، بشكل عام ، لا يتكون بالكامل منها. إذا
لكن الطيف ، بشكل عام ، لا يتكون بالكامل منها. إذا 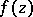 هي وظيفة تحليلية محددة في حي من
هي وظيفة تحليلية محددة في حي من 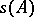 ، و إذا
، و إذا 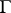 هو كفاف مغلق مغلق
هو كفاف مغلق مغلق 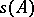 والكذب في مجال تحليل
والكذب في مجال تحليل 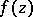 ، ثم يضع واحد
، ثم يضع واحد
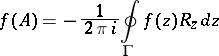 |
والمكالمات 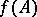 وظيفة المشغل. إذا
وظيفة المشغل. إذا 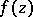 هو متعدد الحدود ، ثم
هو متعدد الحدود ، ثم 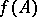 يتم الحصول عليها عن طريق استبدال ببساطة
يتم الحصول عليها عن طريق استبدال ببساطة  في هذا متعدد الحدود من قبل
في هذا متعدد الحدود من قبل 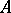 . المراسلات
. المراسلات 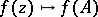 له خصائص تشابهية مهمة:
له خصائص تشابهية مهمة:
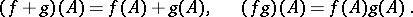 |
وهكذا ، في ظل ظروف محددة على 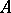 يمكن للمرء أن يحدد ، على سبيل المثال ،
يمكن للمرء أن يحدد ، على سبيل المثال ، 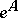 ،
، 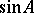 ،
، 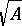 وما إلى ذلك
وما إلى ذلك
من بين فئات خاصة من المشغلين التي تعمل على مساحة Banach 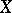 يتم لعب الدور الأكثر أهمية من قبل ما يسمى بالمشغلات المستمرة أو المدمجة تمامًا (cf. المشغل الكامل المستمر ؛ المشغل المدمج ). إذا
يتم لعب الدور الأكثر أهمية من قبل ما يسمى بالمشغلات المستمرة أو المدمجة تمامًا (cf. المشغل الكامل المستمر ؛ المشغل المدمج ). إذا 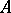 مضغوط ، ثم المعادلة
مضغوط ، ثم المعادلة 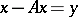 (
( 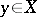 هو ناقلات معينة و
هو ناقلات معينة و 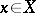 وقد تم دراسة جيدة ناقل). إن نظائر جميع الحقائق التي تحمل المعادلات الخطية في الفراغات المحدودة الأبعاد صالحة أيضاً لهذه المعادلة (ما يسمى نظرية فريدهولم). للمشغلين المدمجة
وقد تم دراسة جيدة ناقل). إن نظائر جميع الحقائق التي تحمل المعادلات الخطية في الفراغات المحدودة الأبعاد صالحة أيضاً لهذه المعادلة (ما يسمى نظرية فريدهولم). للمشغلين المدمجة 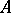 احد الدراسات الظروف التي تضمن أن نظام ناقلات eigen من
احد الدراسات الظروف التي تضمن أن نظام ناقلات eigen من 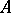 والمتجهات المرتبطة بها كثيفة في
والمتجهات المرتبطة بها كثيفة في 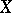 ، أي ، أي متجه في
، أي ، أي متجه في 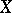 يمكن تقريبها من خلال مجموعات خطية من ناقلات eigen والمتجهات المرتبطة بها ؛ في نفس الوقت ، حتى بالنسبة للمشغلين الصغار ، المشاكل التي تنشأ بشكل طبيعي ولكن يصعب حلها (على سبيل المثال ، نظرية أن كل مشغل من هذا القبيل لديه مساحة فرعية ثابتة
يمكن تقريبها من خلال مجموعات خطية من ناقلات eigen والمتجهات المرتبطة بها ؛ في نفس الوقت ، حتى بالنسبة للمشغلين الصغار ، المشاكل التي تنشأ بشكل طبيعي ولكن يصعب حلها (على سبيل المثال ، نظرية أن كل مشغل من هذا القبيل لديه مساحة فرعية ثابتة 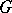 تختلف عن 0 وكل من
تختلف عن 0 وكل من 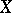 ، وهذا هو ، فضاء جزئي
، وهذا هو ، فضاء جزئي 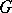 مثل ذلك
مثل ذلك 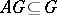 . في حالة متناهية الأبعاد وجود
. في حالة متناهية الأبعاد وجود 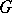 يتبع تافهة من حقيقة أن الطيف غير فارغ).
يتبع تافهة من حقيقة أن الطيف غير فارغ).
طيف مشغل مضغوط 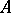 منفصل ويمكن أن يتراكم عند 0 فقط. يميز أحدهما الفئات الفرعية الهامة لفئة المشغلات المدمجة وفقًا للمعدل الذي تقترب به قيم eigen 0. وهكذا ، غالباً ما يواجه المرء مشغلي Hilbert – Schmidt. إذا
منفصل ويمكن أن يتراكم عند 0 فقط. يميز أحدهما الفئات الفرعية الهامة لفئة المشغلات المدمجة وفقًا للمعدل الذي تقترب به قيم eigen 0. وهكذا ، غالباً ما يواجه المرء مشغلي Hilbert – Schmidt. إذا 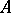 هو المشغل على
هو المشغل على 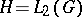 ، ثم هو عامل هيلبرت شميت إذا وفقط إذا كان مشغل متكامل مع النواة
، ثم هو عامل هيلبرت شميت إذا وفقط إذا كان مشغل متكامل مع النواة 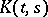 هذا مربع قابل للتلخيص في كلا المتغيرين. كما تمت دراسة مشغلي فولتيرا المدمجة بالتفصيل. كما أجريت دراسة عن المشغلين الطيفيين التي يوجد لها نظير لحل هذه الهوية
هذا مربع قابل للتلخيص في كلا المتغيرين. كما تمت دراسة مشغلي فولتيرا المدمجة بالتفصيل. كما أجريت دراسة عن المشغلين الطيفيين التي يوجد لها نظير لحل هذه الهوية 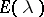 . وما إلى ذلك (انظر [8] ).
. وما إلى ذلك (انظر [8] ).
4. بنبات الجبر ونظرية التمثيل.
في المراحل المبكرة من تطور تحليل الدوال ، كانت المشاكل التي تمت دراستها هي تلك التي يمكن ذكرها وحلها من حيث العمليات الخطية على عناصر المساحة وحدها.
واحدة من الأساليب القوية في الرياضيات هي تمثيل الأشياء الرياضية المجردة بواسطة كائنات أبسط (أو أكثر واقعية). على سبيل المثال ، يمكن تفسير النظرية الطيفية على أنها تمثل عامل التشغيل الذاتي من قبل المشغل الذي يضاعف الوظائف القابلة للقياس لفئة معينة بواسطة المتغير المستقل. إذا أخذنا في الاعتبار الضرب من خلال وظائف بوريل ، يحصل المرء على تمثيل لجبر مقنن تبادلي من المشغلين في فضاء هيلبرت. يعطي مثال أكثر عمومية لهذا التمثيل أحد النظريات الرئيسية في نظرية الجبر التبادلي Banach.
سمح 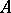 يكون الجبر التبادلي Banach ، من أجل البساطة مع الهوية ، أي مساحة Banach التي يوجد فيها تكاثر تبادلي وتربوي
يكون الجبر التبادلي Banach ، من أجل البساطة مع الهوية ، أي مساحة Banach التي يوجد فيها تكاثر تبادلي وتربوي 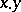 من العناصر
من العناصر 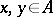 ، والسماح للقاعدة ترضي
، والسماح للقاعدة ترضي 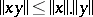 . علاوة على ذلك ، دعونا
. علاوة على ذلك ، دعونا 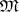 يكون مجموعة من جميع المثل القصوى. ثم يمكن إدخال طوبولوجيا مدمجة
يكون مجموعة من جميع المثل القصوى. ثم يمكن إدخال طوبولوجيا مدمجة 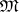 بحيث كل عنصر
بحيث كل عنصر 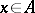 يمثل وظيفة مستمرة ذات قيمة معقدة
يمثل وظيفة مستمرة ذات قيمة معقدة 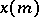 ،
، 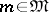 ، وعلاوة على ذلك ، المبلغ
، وعلاوة على ذلك ، المبلغ 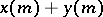 والمنتج
والمنتج 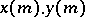 من الوظائف تتوافق مع المبلغ
من الوظائف تتوافق مع المبلغ 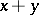 والمنتج
والمنتج 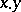 ، على التوالي (انظر [7] ). في دراسة الحالة غير التبادلية تم دراسة نظرية التمثيل خاصة لما يسمى بالجبر مع انبثاق (انظر جبر بانتاخ ).
، على التوالي (انظر [7] ). في دراسة الحالة غير التبادلية تم دراسة نظرية التمثيل خاصة لما يسمى بالجبر مع انبثاق (انظر جبر بانتاخ ).
تم تطوير نظرية تمثيل أكثر ثراء للمجموعات الطوبولوجية (راجع تمثيل مجموعة طوبولوجية ).
5. تحليل الدوال غير الخطي.
وفي نفس الوقت الذي يجري فيه تطوير مفهوم الفضاء وتعميقه ، يجري تطوير مفهوم الوظيفة وتعميمه. في النهاية ، أصبح من الضروري النظر في التعيينات (وليس بالضرورة خطية) من مسافة إلى أخرى. واحدة من المشاكل المركزية في تحليل الدوال غير الخطي هي دراسة مثل هذه التعيينات. وكما هو الحال في الحالة الخطية ، يُطلق على رسم خريطة لمساحة إلى الأرقام (الحقيقية أو المعقدة) اسم وظيفي. بالنسبة إلى التعيينات غير الخطية (على وجه الخصوص ، الوظائف غير الخطية) ، هناك طرق مختلفة لتعريف مفاهيم التفاضل ، والمشتق الاتجاهي ، وما إلى ذلك ، مماثلاً للمفاهيم المقابلة في التحليل الرياضي التقليدي (انظر [11] ، [13 ] ، [15] وتمييز رسم الخرائط ).
هناك مشكلة مهمة في تحليل الدوال غير الخطي هي مشكلة تحديد النقاط الثابتة في رسم الخرائط (انظر [11] ، [13] ، [15] والنقطة الثابتة .
عند دراسة متجهات موجية لرسم الخرائط غير الخطية التي تحتوي على معلمة ، تنشأ ظاهرة حاسمة في التحليل غير الخطي – ما يسمى بالتشعب (انظر [15] ).
في التحري عن النقاط الثابتة ونقاط التشعب ، تستخدم الطرق الطوبولوجية على نطاق واسع: التعميم إلى الفراغات اللانهائية الأبعاد لنظرية Brouwer –Bohl على وجود نقاط ثابتة لتعيينات المساحات المحدودة الأبعاد ، فهرس رسم الخرائط (cf صيغ الفهرس ) ، إلخ.
6. تطبيق تحليل الدوال في الفيزياء الرياضية والنظرية.
أدناه ، يتم إعطاء تلك الفروع من الفيزياء الرياضية التي يتم فيها تطبيق بعض جزء من تحليل الدوال.
1) يتم تطبيق النظرية الطيفية للمشغلين في جميع نظريات الفيزياء الكوانتية: في الكم  نظرية الشخص ، في نظرية المجال الكمي وفي الميكانيكا الإحصائية الكمية. بالإضافة إلى ذلك ، يتم تطبيق نظرية طيفية في دراسة نماذج الأنظمة الديناميكية في الميكانيكا الكلاسيكية ، في دراسة المعادلات الخطية في الديناميكا المائية ، في دراسة حقول غيبس ، إلخ.
نظرية الشخص ، في نظرية المجال الكمي وفي الميكانيكا الإحصائية الكمية. بالإضافة إلى ذلك ، يتم تطبيق نظرية طيفية في دراسة نماذج الأنظمة الديناميكية في الميكانيكا الكلاسيكية ، في دراسة المعادلات الخطية في الديناميكا المائية ، في دراسة حقول غيبس ، إلخ.
2) يتم تطبيق نظرية التشتت في فيزياء الكم. تجدر الوالله اعلم ربما يحتمل ان تكون اشارة الى أن النظرية الرياضية الحديثة من نثر نشأت في المقام الأول في الفيزياء. في السنوات الأخيرة ، تم تطبيق نظرية التشتت (المشكلة العكسية) في دمج معادلات النماذج غير الخطية في الفيزياء الرياضية.
3) يتم تطبيق جزيئات Banach في نظرية المجال الكمي ، وخاصة في ما يسمى نظرية المجال البدهي ، وفي دراسة نماذج متكاملة متعددة من حقل كمي وميكانيكا إحصائية. كما تستخدم الجبر فون نيومان في هذه الأسئلة.
4) نظرية التشويش ، وهي أساسًا نظرية التشويش على المشغلين الخطيين ، يتم تطبيقها في جميع مجالات الفيزياء الرياضية تقريبًا: في نظرية المجال الكمي وفي الميكانيكا الإحصائية ، كلاً من التوازن وعدم التوازن (خاصة في دراسة المعادلات الحركية المزعومة ، الأطياف المركبة للأنظمة متعددة الجسيمات ، وما إلى ذلك).
5) يتم تطبيق تكامل االدوال والمقاييس في الفراغات الوظيفية في نظرية المجال الكمي البناء وفي الميكانيكا الإحصائية الكمية.
6) يتم تطبيق العديد من التمثيلات المتكاملة (نظرية رييز ، ونظرية كيلين-ميلمان ، ونظرية شوكيه ، وغيرها) في نظرية مجال الكم البصري وفي الميكانيكا الإحصائية.
7) يتم تطبيق مسافات ناقلات (أساسا مسافات هيلبرت) في نظرية الكم وفي الفيزياء الإحصائية.
8) يتم تطبيق الوظائف المعممة في كل مكان في الفيزياء الرياضية كأداة تحليلية مهمة (انظر أيضا وظيفة معممة ). وبذلك يكون انتهينا من بحث عن تحليل الدوال
اقرأ ايضا
تعرف على نظام كلاسيرا التعليمي ومميزاته الكبيرة








التعليقات